For those of you who don’t know, Flare-On is an annual “reverse engineering marathon” organized by Mandiant (formerly by FireEye). It runs for 6 weeks, and contains usually 10-12 tasks of increasing difficulty. This year I completed as 103 (solves board here). In this short series you will find my solutions of the tasks I enjoyed the most.
Time for some crypto challenge:
You can find the package here: 09_encryptor.7z , password:
flare
After unpacking the archive we see:
It is a 64-bit PE – “a ransomware”, plus a file encrypted by it, that needs to be recovered. So, we have an emulation of the ransomware decryption scenario.
I used to crack ransomware in the past, and I still find this kind of cryptoanalysis tasks very enjoyable. As usually in such cases, two algorithms are used:
- symmetric, to encrypt a file (with a random key)
- asymmetric, to protect the generated random key
A flaw can be in one of the following:
- how the random key is generated (was the strong random generator used?)
- how the symmetric encryption is implemented (any implementation flaws making it weaker?)
- how the asymmetric encryption is implemented
- finally: are the algorithms applied correctly?
The task is written in C, and the code is pretty small, and focused on the main goal, so the analysis is easy.
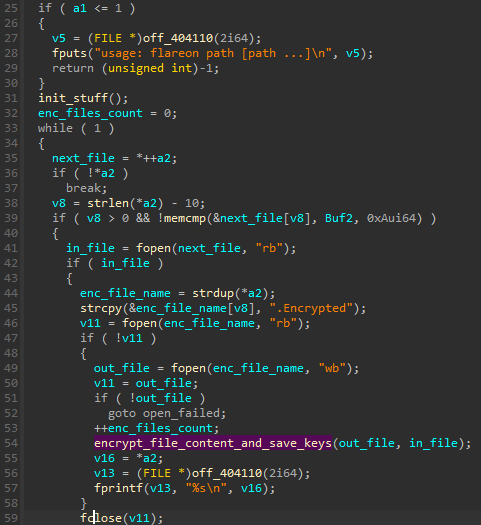
The file is encrypted with ChaCha:
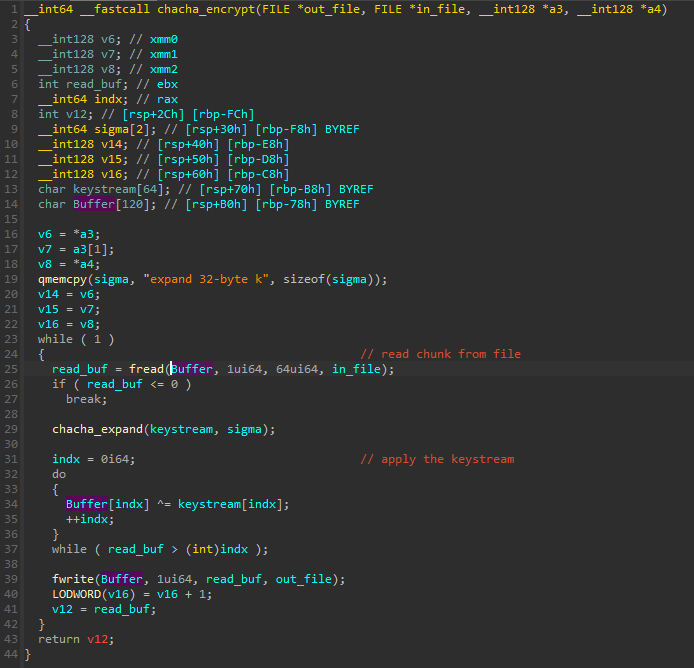
This version of ChaCha uses 32 byte key, and 12 byte nonce. The implementation of ChaCha seems correct. Also, for the generation of the key and nonce, a strong random generator is used (SystemFunction036). So at this point my guess is that the bug must be somewhere around the asymmetric algorithm.
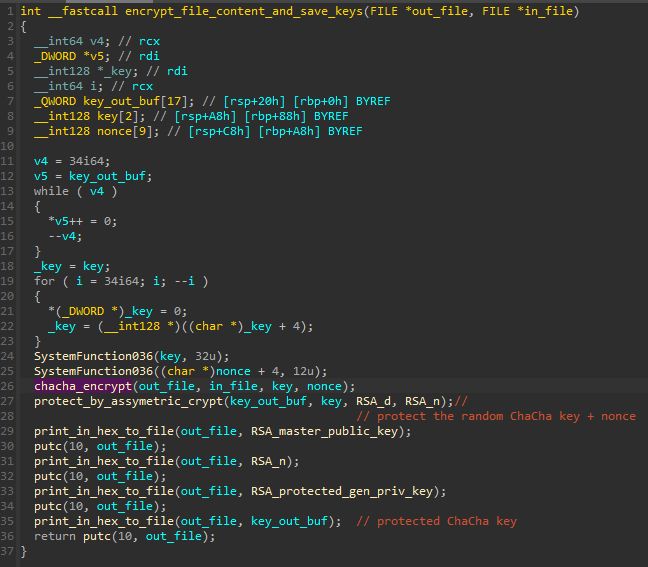
After the file is encrypted, the buffer containing the key and nonce is encrypted with a private key from a newly generated keypair.
So, the 4 hex strings that we see at the end of the file suppose to contain the following elements:
{RSA master public key - the hardcoded master public key}
{RSA generated public key - the public key from the generated keypair}
{RSA generated private key, protected by the RSA master public key}
{ChaCha key and nonce, protected by the RSA generated private key}If everything is correct there, we need the RSA master private key, in order to decrypt the RSA generated private key, in order to decrypt the ChaCha key and nonce… Let’s take a closer look if it really is this way.
A good cheatsheet describing all the RSA building blocks is available here.
Snippet describing the parts related to RSA implementation:
I made a small loader for the original app, and hooked the functions with detours (loader.cpp), in order to quickly log all their input and output parameters. At some point, I noticed something very suspicious: instead of the generated private key being provided to encrypt the generated ChaCha key, what was passed was the standard public exponent! So, in reality is is RSA signing.
To recover the “encrypted” content, all we have to do is to use the exponent 10001 as a private key.
For solving the final equation, I used the following online tool: https://www.boxentriq.com/code-breaking/rsa
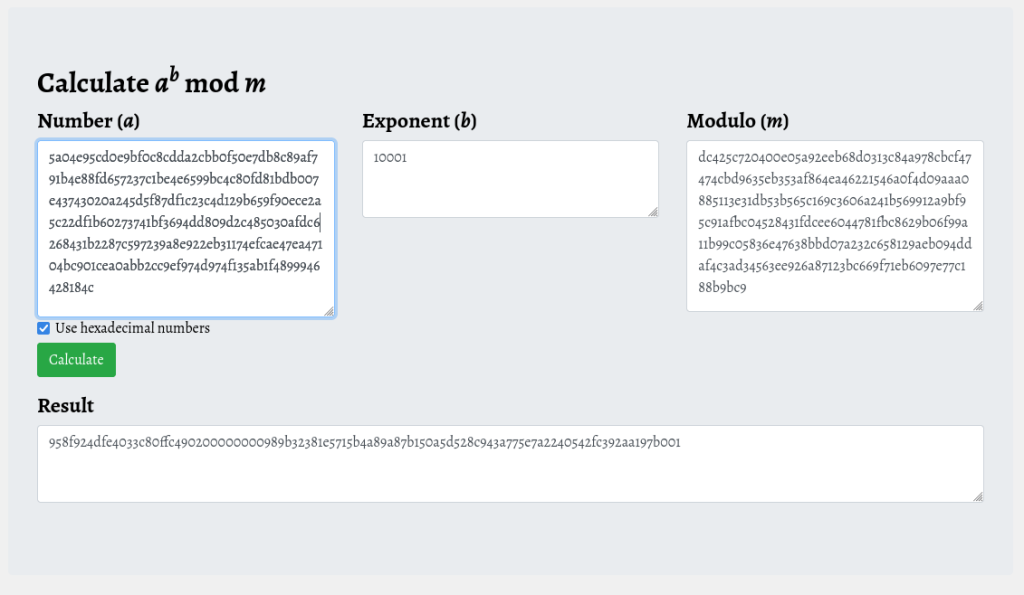
By looking at the output we can see that it is in the correct format of key and nonce. However, we still need to reverse the bytes before using.
Now in order to decode the file content, we can just rename the file to “.EncryptMe” and we can set a breakpoint after the key and nonce are generated, to replace them in memory.
And we get the original content decrypted:
Hello! The flag is: R$A_$16n1n6_15_0pp0$17e_0f_3ncryp710n@flare-on.com
